Introduction

ACMS has developed state-of-the-art numerical algorithms for solving 3D time domain and spectral vector Maxwell simulators. The software we develop employs the most advanced and computationaly effcient methods based on adaptive structures mesh refinement FDTD, high order vectorial and discontinuous Galerkin spectral finite element mehods in both frequency and time domain.

These methods improve dramatically overall effciency and accuracy in comparison to conventional finite difference and finite element methods. These simulators can model electro-magnetic waves over time (such as light, radiation, etc) and play an important role in developing optical devices as well as many other applications. We focusus on designing efficient parallel supercomputing algorithms for sub-wavelength scale light propagation and intercation throught composite materials, including dispersive materials and metal/dielectric intefaces.

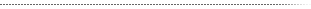
Grid refinement

Continuous reduction in the feature size of the integrated optical components and experimental advances in the field of photonic nano-circuits necessitate smaller FDTD grid cell size in order to provide adequate resolution of the geometry.

When there are small, localized geometric features, or when multiple integrated device components are modeled, a computational mesh with variable grid size is desired. The main advantage of the methods based on such grid refinement is an improved resolution and computation efficiency over the methods that use uniform mesh size.

References

• A.R. Zakharian, M. Brio, C. Dineen and J.V. Moloney, "Second order accurate 3D FDTD space and time grid refinement method", Phot. Tech. Lett. 18(11), pp. 1237-1239, 2006
• A.R. Zakharian, M. Brio, C. Dineen and J.V. Moloney, "Application of the finite-difference time-domain (FDTD) method with local grid refinement to nanostructure design" Proceedings of SPIE 5728, 154 (2005), DOI:10.1117/12.590765

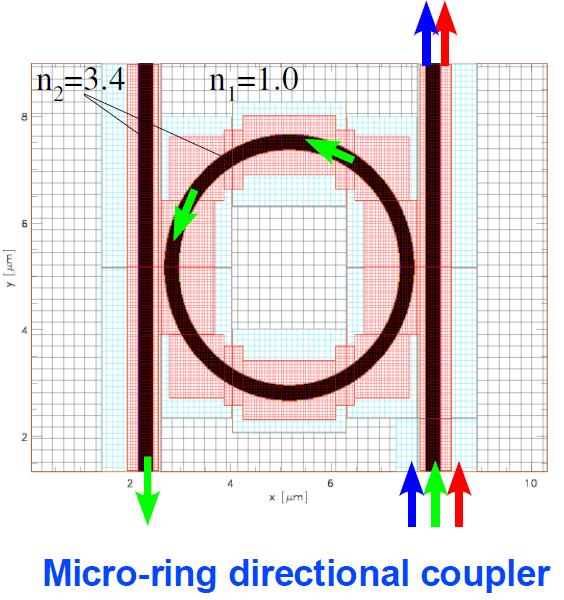
Non-uniform mesh FDTD

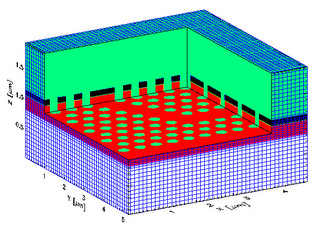
A fully 3D non-uniform mesh FDTD solver is extensively used to simulate light interactions with 3D photonic crystal structures, nanowire pair arrays (search for negative index materials) and, light transmission through nano metallic apertures for high density optical data storage.

ACMS researchers also have developed a 3D Adaptive space and time mesh algorithm that places refined meshes on nano-scaled features while cascading to progressively coarser mesh away from some features. A major thrust of the Center research activity has been the development of realistic material models that capture the electromagnetic response of very large spectral bandwidths associated with ultra-short pulse interaction with nonlinear materials.

References

• A.R. Zakharian, J.V. Moloney and M. Mansuripur, "Interaction of Light with Subwavelength Structures", Optics and Photonics News., pp 56-61 March 2003
• A.R. Zakharian, J. Hader, J.V. Moloney, S.W. Koch, P. Brick and S. Lutgen, "Experimental and Theoretical Analysis of Optically Pumped Semiconductor Disc Lasers", Applied Physics Lett., 83, pp. 1313-1315 (2003)

Adaptive Mesh Refinement

A grid refinement method developed at the ACMS is based on a hierarchy of nested grid levels, refined recursively by a ratio of two, in Cartesian space coordinates and in time. The grid is usually refined in the areas with large gradients in the solution, in particular around the material interfaces, and in the regions that have large refractive index, where the wavelength is shorter, and hence higher resolution is beneficial.

In the last two decades there have been numerous attempts to improve computational efficiency of FDTD for sub-wavelength structures by using local space and time grid refinement strategies to resolve sub-wavelength geometrical features. Such situations are common when modeling nanoscale photonic structures containing quantum dots, photonic crystal microcavities, optical data storage marks, thin metal films, and small apertures.

Maximum improvement in the computational cost is possible when using both space and time grid refinement, when each grid refinement level advances solution with its own time step, computed from the stability criteria for the FDTD method with a given spatial The computational advantages of local space and time grid refinement methods are well documented, and their effective application produces numerical results comparable to that of using the finest mesh uniformly over the whole domain.

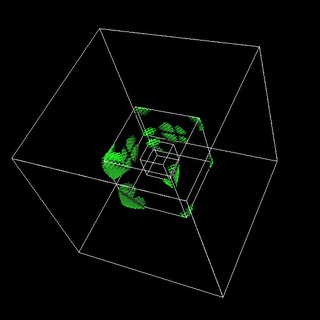In FDTD AMR Maxwell code the desigh of satble and accurate interface boundary conditions is the key issue to achieve accurate results for long time simulations. The multilevel approach, refinement both inspace and time, allows to subcylcle on the small number of fine grid patches resulting in improved spped up and while preserving the accuracy of the computation as if it were done on the unifirom grid with fine resolution.

Incorporation of cut and patially filled cells, for dielectric and perfectly conducting surfaces, especially metal filled cells are need for improved resolution and errors reduction due to complex geometrical structures of the optical nanostructure devices. Implementation of these steps will remove the staircasing effect in conventional approaches.

The AMR Vector Maxwell code developed at the ACMS is an extension of the adaptive mesh refinement (AMR) procedure, originally developed for hyperbolic conservation laws, to the staggered space-time FDTD scheme. Using AMR, cartesian grids are refined around fine-scale structures to increase the resolution of the solution and focus computational resources on the regions of interest. Local grid refinement in both space and time reduces the memory and computational requirements when compared to traditional uniform mesh discretization while preserving the accuracy of the computation as if it were done on the uniform grid with fine resolution.

Parallel AMR algorithms on distributed memory architectures, however, present a number of implementation issues not encountered in non-AMR implementations of the FDTD method. The main implementation difficulties lie in data representation and management of the nested grid hierarchy, dynamic communication of data across grids at the same refinement level and between grids at different levels of refinement, and load balancing the distribution of refined grids across processors in order to minimize data communication and maximize processor utilization.

In AMR FDTD codes the design of stable and accurate coarse-fine interface boundary conditions is the key issue to achieve accurate results for long time simulations. The code implements a second order accurate formulation based on high order interpolations, and enforces conservation of the magnetic field circulation at the fine-coarse grid boundaries. Additional AMR FDTD code enables different regions of the computational domain be filled with phenomenologically different optical materials. A range of numerical material models may be accommodated including simple dielectric, dispersive, non-linear or active materials. Particular attention has been paid to facilitatg the development of a graphical user interface for 3D geometry layout and material selection.

References

• A.R. Zakharian, M. Brio, C. Dineen and J.V. Moloney, "Second order accurate 3D FDTD space and time grid refinement method", Phot. Tech. Lett. 18(11), pp. 1237-1239, 2006
• A.R. Zakharian, M. Brio, C. Dineen and J.V. Moloney, "Stability of 2D FDTD algorithms with local mesh refinement for Maxwell's equation" Comm. Math. Sci. 4(2) (2006)
• A.R. Zakharian, M. Brio, C. Dineen and J.V. Moloney, "Application of the finite-difference time-domain (FDTD) method with local grid refinement to nanostructure design" Proceedings of SPIE 5728, 154 (2005), DOI:10.1117/12.590765
• J.V. Moloney, A. R. Zakharian, C. Dineen, and M. Brio, "AMR FDTD solver for nanophotonic and plasmonic applications", Proc. SPIE 5451, 97 (2004), DOI:10.1117/12.548983

Overlapping Yee FDTD Method on Nonorthogonal Grids

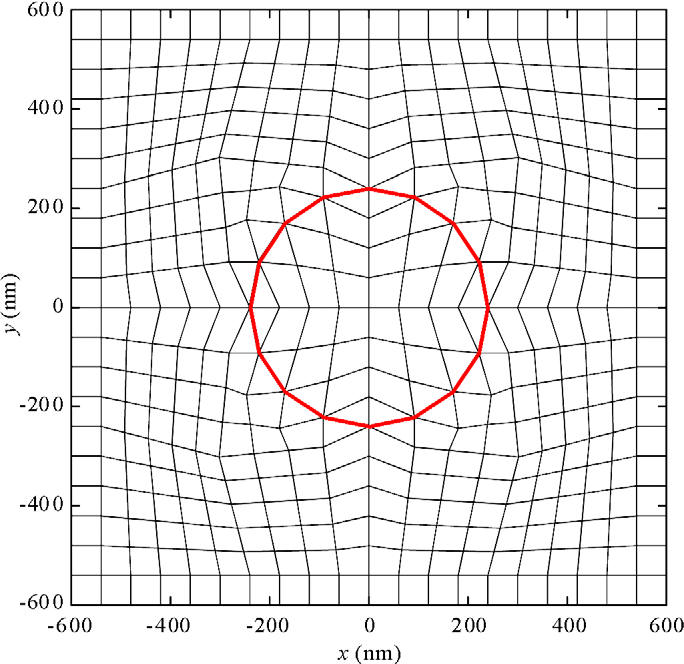The ACMS has also developed a new overlapping Yee (OY) method for solving time-domain Maxwell equations on nonorthogonal grids. The proposed method is a direct extension of the Finite-Difference Time-Domain (FDTD) method to irregular grids. The OY algorithm is stable and maintains second-order accuracy of the original FDTD method, and it overcomes the late-time instability of the previous FDTD algorithms on nonorthogonal grids.

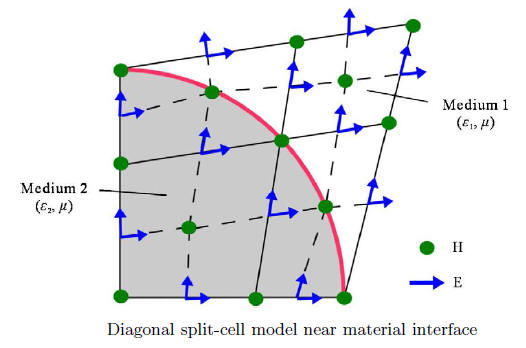In cases, where physical quantities of interest depend on accurate field values at curved surface, the FDTD method may revert to first order and even may not converge to the correct solution, while our method has definite advantages in that it always converges to the correct solution, It is more accurate and more efficient and it overcomes the late-time instability problem of other nonorthogonal FDTD algorithms. In our current implementation for general nonorthogonal mesh, the edge centers on the original cells and the corresponding edge centers on the overlapping cells may not locate exactly at the same position. As a result, the local error in term of L-norm is first order, while the global error in term of L-norm is still second order.

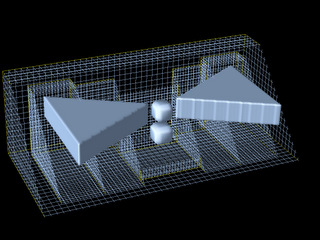
The algorithm maintains the Yee-type data structure and can be parallelized in the same fashion. On the orthogonal grid the algorithm is reduced to standard FDTD method. An even better efficiency can be achieved if OY algorithm is used in conjunction with adaptive mesh FDTD method (AMR-FDTD) to resolve the small curved structures. In this case, the method will be used only over small regions on the finest levels of mesh refinement. Currently, we are applying our method to the computation of optical forces and resonances to the metallic nanostructures, such as the metallic bowtie nanoantennas consisting of two opposing gold triangles.

Refrences

• Jinjie Liu , Moysey Brio, and Jerome V. Moloney, "Overlapping Yee FDTD Method on Nonorthogonal Grids", J. Sci. Comput., 39 (1), 129-143, 2009. DOI: 10.1007/s10915-008-9253-1.
• Jinjie Liu, Moysey Brio, Jerome V. Moloney, "A Diagonal Split-cell Model for the Overlapping Yee FDTD Method", Acta Mathematica Scientia, 29 B (6), 1670-1676, 2009. DOI: 10.1016/S0252-9602(10)60009-4.

Light Matter Interaction

We also research fundamental isssues in gaining an understanding of the physics of light interacting with nano-featured semiconductors and metals is a proper physically self-consistent microscopic approach. ACMS researchers, in collaboration with the Condensed Matter theory group at the University of Marburg, Germany have developed the only truly predictive description of light interaction with semiconductor quantum well materials. A goal of the present work will be to develop an equally sophisticated microscopic approach to the study of electron-ion plasmas in nanometals.

References

• J. Hader, S. W. Koch, J. V. Moloney, "Microscopic theory of gain and spontaneous emission in GaInNAs laser material", Solid-State Electronics, Volume 47, Issue 3, March 2003, Pages 513-521, ISSN 0038-1101, DOI: 10.1016/S0038-1101(02)00405-7.
• J. Hader, J. V. Moloney, S. W. Koch, "Microscopic Evaluation of Spontaneous Emission- and Auger-Processes in Semiconductor Lasers", IEEE Journal of Quantum Electronics, vol. 41, issue 10, pp. 1217-1226

Integral formulations of the Maxwell equations

A large class of computational problems in optics, and photonics in particular, involves the scattering of light by linear materials that have piecewise constant material constants. In many cases the light sources are approximately monochromatic. It is furthermore typically the case that the values of the electric and magnetic field components are only needed in a limited part of what is usually a noncompact domain. This is in particular true for near-field optics and for the calculation of resonances and optically induced forces.

In all these cases the Muller equations, an integral formulation of the Maxwell equations, are optimal in the sense that they involve only degrees of freedom that are needed to calculate quantities of physical interest and no more. We have developed a highly efficient MPI based parallel implementation of the Muller equations for multiple spheres that runs on a large computational cluster.

This project will develop an algoritm for solving the Muller equations for general surfaces by triangulating the surfaces. Combinations of waveguides and various compact objects are of particular interest. Our goal is to derive the coupled surface-volume integrodifferential equations for transient scattering from a combination of linear homogenous, linear inhomogenous and nonlinear scattering objects.

We also develop algoritms for solving the equations for various situations of scientific and technological interest, and extend the integral approach to the calculation of Casimir forces for nanostructures of complex geometrical shape and physical material properties.

References

• Per Jakobsen,"Calculating Optical Forces using the Boundary Integral Method", Physica Scripta 2009 ;Volum 80.(3)

Nonlinear Drude Model

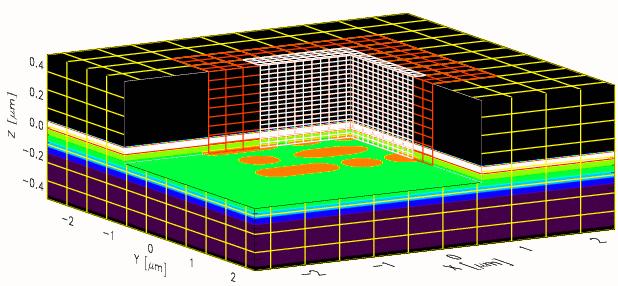
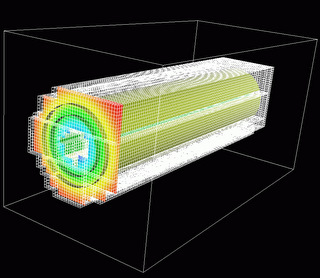
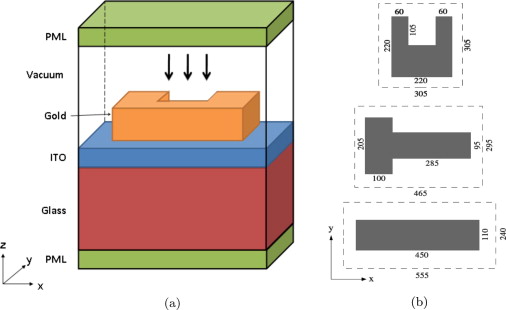The ACMS has developed a numerical method for solving a three-dimensional cold-plasma system that describes electron gas dynamics driven by an external electromagnetic wave excitation. The nonlinear Drude dispersion model is derived from the cold-plasma fluid equations and is coupled to the Maxwell field equations. The Finite-Difference Time-Domain (FDTD) method is applied for solving the Maxwell equations in conjunction with the time-split semi-implicit numerical method for the nonlinear dispersion and a physics based treatment of the discontinuity of the electric field component normal to the dielectric-metal interface. The application of the proposed algorithm is illustrated by modeling light pulse propagation and second-harmonic generation (SHG) in metallic metamaterials (MMs). The Figure shows the computational domain for light pulse propagation through three dimensional gold nanostructures with ITO and glass substrates; (b) x-y cross-sections of U-shaped, T-shaped and rectangular gold nanostructures (units shown in nm).

References

• Jinjie Liu, Moysey Brio, Yong Zeng, Armis Zakharian, Walter Hoyer, Stephan W. Koch, Jerome V. Moloney, "Generalization of the FDTD algorithm for simulations of hydrodynamic nonlinear Drude model", J. Comput. Phys., 229, 5921-5932, 2010. DOI: 10.1016/j.jcp.2010.04.016.

Beyond the NLS description of Light Strings

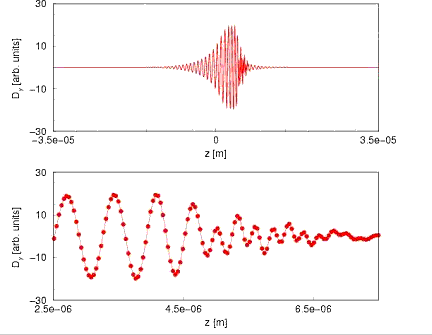The Nonlinear Schrodinger Equation (NLSE) is ubiquitous as a description of weakly nonlinear dispersive behavior in diverse physical systems. In nonlinear optics it can be obtained from Maxwell's equations as an envelope description of optical pulse propagation through an asymptotic expansion in powers of an appropriate small parameter. Additional correction terms that become important for shorter pulse durations can be systematically obtained in a similar fashion. However, it has been critically important to obtain a mathematical model of ultrashort high power pulse propagation in situations where the NLS description fails and yet, Maxwell s equations remain untenable as a computationally feasible model.

References

• M. Kolesik, J. V. Moloney, and M. Mlejnek, "Unidirectional optical pulse propagation equation", Phys. Rev. Lett.,Volume 89, Issue 28
• M. Kolesik, and J. V. Moloney, "Nonlinear optical pulse propagation simulation: From Maxwell's to unidirectional equations", Phys. Rev. E 70, 036604 2004

Home