Introduction

Our primary compute server is a UV2000 from Silicon Graphics (right). This latest generation computer, released June 2012 and installed at the ACMS in September 2012, is scalable, coherent shared memory computer. The SGI UV2000 operates just like a single workstation (on one system image any program has access to all the cores and all the memory of the system); it is far less complex to program than traditional cluster systems with many distrobuted nodes. The ACMS UV2000 contains 32 Intel Xeon E5-4600 Processor, 6 core, 2.9GHz for a total of 192 cores. It has 2 TBytes Main Memory, 12 TBytes SAS fast disk storage and 16 Tbytes network attached storage. The system also integrates 8 nVidia M2090 GPUs each with 512 CUDA cores and 6 Gbytes of on board memory.

Our secondary compute server is a SGI Altix XE cluster from Silicon Graphics (left). This cluster contains 36 Intel Xeon E5420 Quad Core Processors for a total of 144 cores. Each processor supports a super-fast 1600 MHz front-side bus and the cluster has combined capacity of 368GBytes of FBDIMM memory. The cluster uses an InfiniBand interconnect that is optimized for high performance computing (HPC) applications.

The ACMS also possess a number of GPU-based Tesla workstations. These workstations contain Dual Intel E5-2690 2.9GHz Eight Core processors and 64GB memory. Each workstation contains up to four Tesla C2075 GPUs each capable of more than 500 gigaflops of double precision performance and 1 teraflop of single precision performance. These CPU-GPU workstations deliver cluster level performance and achieve up to 250 times the performance of a standard workstation.

Current projects at ACMS are based on 3D vector Maxwell FDTD, FFT, or FEM modal analysis. All projects require large computational resources in terms of memory and CPU. These codes exhibit non-local data access patterns making parallel implementation on shared memory architectures significantly simpler from a programming point of view. The high performance computing facilities at the ACMS significantly reduce the software development time and improve the performance of the ACMS simulation software.

VECSEL Modeling

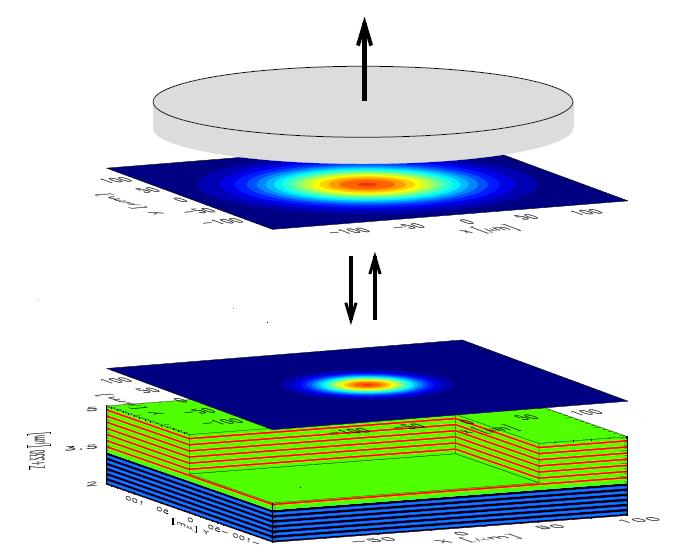
Modeling thermal properties of the optically pumped VECSEL requires solution of coupled PDEs, describing heat generation and transfer through the device, and carrier transport in the QWs, in at least two space dimensions. Accurate estimation of the temperature distribution in the active layer of the multi-QW VECSEL depends on the realistic model representation of the heat transport through the device substrate and the heat sink, which leads to computations with large number of spatial grid cells.

In addition, the carrier localization in the QWs necessitates small grid cell size in the active layer of the device, further increasing the computational problem size. The discretization of the equations leads to a large, sparse linear system of equations, suitable for solution using iterative solvers. The software developed for the simulation of the thermal properties of VECSELs is based on Aztec library - a massively parallel, iterative solver for sparse linear systems (available from Sandia National Lab).

Benchmark of the code for modeling thermal properties for problems with constant number of grid points per CPU, indicates better > 90% speedup on up to 16 CPUs. Comparison of the performances on systems with faster processors indicates that near linear improvement in computation time can be projected with the improved processor speed. Further development of the model will include addition of the effects of the optical field on the lasing properties of the VECSEL due to field dependence on the transverse coordinate. Numerical solution of the field equations representing this effects can take advantage of the parallel FFT libraries, optimized for shared memory architecture.

FDTD

Simulation of the photonic components, with feature sizes on the scales comparable to the wavelength of light, requires full vector solution of the classical electrodynamics equations in 2- or 3-D.

One such problem is interaction of the focused laser beam with phase-change layer of the optical disk data storage system. Large domain size (20*lambda x 20*lambda) and number of points (800x800x100 cells, even with non-uniform grid resolving the region of the focused spot) lead to large memory requirement and long simulation times.

Two-three point time step storage typical for the models of the dispersive material properties in the time domain, limits the size of the problem that can addressed with the FDTD method. The memory limitation also becomes dominant for problems that require high resolution in the spatial frequency domain, requiring large computational domain size.

Due to scalability, the FDTD computations will benefit linearly from both the improved clock speed and nearly six times larger memory of the new system.

Adaptive Mesh Refinement FDTD

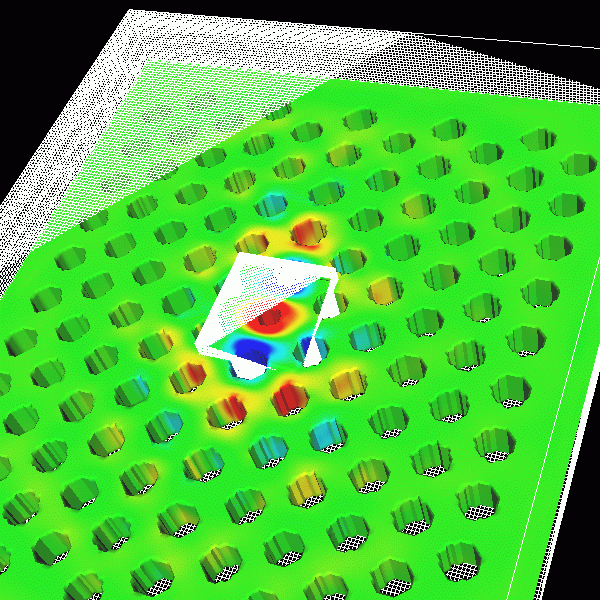
An alternative approach suitable for simulations involving large FDTD computational domains is to employ Adaptive Mesh Refinement (AMR).

AMR algorithms represent the computational domain as a set of nested, locally refined grids. The AMR approach can reduce the memory and computational requirements when compared to traditional uniform mesh discretization.

In AMR, cartesian grids are refined around fine-scale structures to increase the resolution of the solution and focus computational resources on the regions of interest. However, AMR algorithms present a number of parallel implementation issues, particularly on distributed memory architectures, not encountered in non-AMR implementations of FDTD method. The main implementation difficulties lie in representation and data management of the nested grid hierarchy, dynamic communication of data across grids at the same refinement level and between grids at different levels of refinement, and load balancing the distribution of refined grids across processors in order to minimize data communication and maximize processor utilization. Some, though not all of these implementation issues are simplified in a shared memory architectures.

Photonic crystal fibers

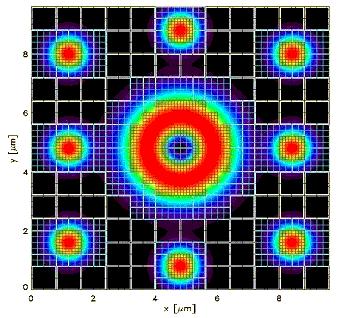Photonic crystal fibers (PCF) are complex structures with the potential to be used as single mode, large-core, compact high-power lasers. In order to simulate these structures with such complicated geometries, one needs to use the finite elements method (FEM).

It is possible to simulate only the overly simplified versions of the PCF on available high speed single processor machines. Any attempt to simulate the PCF in 3 dimensions or even complicated geometries in 2 dimensions requires much faster computation power along with significantly greater memory capacity.

In a complicated PCF structure, especially in 3-D, the FEM stiffness matrix is built on the whole domain of computation. For small scale problems, software libraries, such as ARPACK, can be used to diagonalize the FEM matrices and find the relevant eigenvalues and eigenvectors.

Some capabilities of the ARPACK software package, such as the ability to solve symmetric, non-symmetric, and generalized eigenproblems are of significant importance in our FEM simulations. For solving large scale eigenvalue problems, the matrices can become prohibitively large requiring efficient parallel matrix solvers. Matrices on the order of a few hundred thousand by a few hundred thousand are common.

In higher order FEM these matrices tend be less sparse and defeat the memory locality assumptions of many sparse matrix solvers. Efficient parallel matrix solvers are easier to implement on shared memory multiprocessors, tests of a parallel implementation of ARPACK on SGI machines show near 90% efficiency.

Home